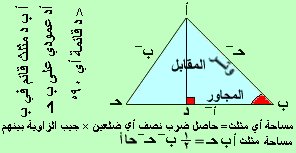
 |
المقابل أ د
ظل الزاوية ب: طاب = ـــــــــــــــ أي طا ب = ــــــــ
المجاور ب د |
المقابل أ د
جيب الزاوية ب: حاب = ـــــــــــــــ أي حاب = ـــــــــ
الوتــــر أ ب |
المجاور ب د
جيب تمام الزاوية ب: حتاب=ـــــــــــــــ أي حتا ب= ـــــــ
الوتــــر أ ب |
| أ + ب + حـ = 180ه |
المجاور ب د
ظل تمام الزاوية ب: طتاب =ــــــــــــــ أي طتا ب= ـــــــ
المقابل أ د |
| أ ، ب زاويتان متتامتان ↔أ + ب = 90ه |
الوتــــر أ ب
قاطع تمام الزاوية ب: قتاب =ـــــــــــــ أي قتا ب= ــــــ
المقابل أ د |
إذا كان: أ + ب = 90ه
فــــــإن: حاأ = حتاب ، طاأ= طتاب ، قاأ = قتاب |
الوتــــر أ ب
قاطع الزاوية ب: قاب = ـــــــــــــــ أي قاب = ـــــــــ
المجاور ب د |
للتحويل من التقدير الدائري للستيني والعكس نستخدم
هـد س˚ 22
ــــــــــ = ــــــــــــ ( هـد دائري ، س˚ ستيني )، ط = ــــــ
ط 180ه 7 |
النسبة × مقلوبها = 1 أي:
طاب × طتاب =1، حاب× قتاب = 1، حتاب× قاب =1 |
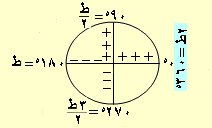 | قيم النسب الستة موجبة في الربع الأول لأي زاوية هـ |
| حاهـ ، مقلوبها موجبة في الربع الثاني والباقية سالبة |
| طاهـ ، مقلوبها موجبة في الربع الثالث والباقية سالبة |
| حتاهـ ، مقلوبها موجبة في الربع الرابع والباقية سالبة |
حا–هـ = – حاهـ ، حتا–هـ = حتاهـ ، طا–هـ = – طاهـ | قتا–هـ = – قتاهـ ، قا–هـ = قاهـ ، طتا–هـ = – طتاهـ |
| حا(90ه – هـ) = حتاهـ ، حتا(90ه – هـ) = حاهـ | طا(90ه – هـ) = طتاهـ ، طتا(90ه – هـ) = طاهـ |
| قا(90ه – هـ) = قتاهـ ، قتا(90ه – هـ) = قاهـ | حا(90ه + هـ) = حتاهـ ، حتا(90ه + هـ) = – حاهـ |
| طا(90ه + هـ) = – طتاهـ ، طتا(90ه + هـ) = – طاهـ | قا(90ه + هـ) = – قتاهـ ، قتا(90ه + هـ) = قاهـ |
| حا(180ه – هـ) = حاهـ ، حتا(180ه – هـ) = – حتاهـ | طا(180ه – هـ)= – طاهـ ، طتا(180ه – هـ)= – طتاهـ |
| قا(180ه – هـ) = – قاهـ ، قتا(180ه – هـ) = قتاهـ | حا(180ه + هـ)= – حاهـ ، حتا(180ه + هـ)= – حتاهـ |
| طا(180ه + هـ) = طاهـ ، طتا(180ه + هـ) = طتاهـ | قا(180ه + هـ) = – قاهـ ، قتا(180ه + هـ) = – قتاهـ |
بنفس الطريقة للزاويتين (270ه ± هـ) وأن قيم نسب 360 ه هي نفس قيم نسب 0ه ومن حيث في أي مثلث:
أ + ب + حـ = 180ه أي أ + ب = 180ه – حـ فإن حتا(أ+ب)= حتا(180ه– حـ)= – حتاحـ ويمكن استنتاج الباقي
وعلى العموم تكتب إشارة النسبة حسب الربع الواقعة فيه الزاوية بعد وضعها على الصورة (م×90± هـ)، م موجبة، هـ حادة ونكتب نفس النسبة (حا) إذا كانت م عدداً زوجياً والنسبة المتممة إذا كانت م عدداً فردياً (حتا).
|
| الزوايا الخاصة: 0ه ، 30ه ، 45ه ، 60ه ، 90ه ، 180ه ، 270ه ، 360ه ، دائرة الوحدة وأي نقطة عليها (س، ص) |
 |
| حا2هـ + حتا2هـ = 1 | ا + طا2هـ = قا2هـ |
| 1 + طتا2هـ = قتا2هـ | حا(أ ± ب) = حاأ حتاب ± حتاأ حاب |
| حتا(أ + ب) = حتاأ حتاب – حاأ حاب | حتا(أ – ب) = حتاأ حتاب + حاأ حاب |
طاأ + طاب
طا( أ + ب) = ـــــــــــــــــــــــ
1 – طاأ طاب |
طاأ – طاب
طا( أ – ب) = ـــــــــــــــــــــــ
1 + طاأ طاب |
| حتا(ب – حـ) × حتا(ب + حـ) = حتا2ب + حتا2حـ – 1 | حا(ب + حـ) × حا(ب – حـ) = حا2ب – حا2حـ |
| حا2حـ = 2حاحـ حتاحـ | حتا2حـ= حتا2حـ – حا2حـ= 2حتا2حـ – 1=1–2حا2حـ |
2طاحـ
طا2حـ = ــــــــــــــــــــ
1 – طا2حـ |
طاحـ – طا3حـ
طا3حـ = ـــــــــــــــــــــــــــــ
1 –3طا2حـ |
| حتا3حـ = 4حتا3حـ – 3حتاحـ | حا3حـ = 3حاحـ – 4حا3حـ |
2ل حـ
حاحـ = ــــــــــــــــ حيث ل = طا ــــــ من ضعف الزاوية
1+ ل2 2 |
1 – ل2 حـ
حتاحـ = ــــــــــــــــ حيث ل = طا ــــــ من ضعف الزاوية
1+ ل2 2 |
| 2حتا2حـ = 1 + حتا2حـ (هامة للتكامل) | 2حا2حـ = 1 – حتا2حـ (هامة للتكامل) |
ب + د ب – د
حاب + حا د = 2حا ـــــــــــــــ حتا ـــــــــــــ
2 2 | ب + د ب – د
حاب – حا د = 2حتاـــــــــــــــ حا ـــــــــــــ
2 2 |
ب + د ب – د
حتاب + حتا د = 2حتا ــــــــــــــ حتا ـــــــــــــ
2 2 |
ب + د ب – د
حتاب – حتا د = –2حا ـــــــــــــ حا ـــــــــــــ
2 2 |
2حاب حتا د = حا( ب + د) + حا( ب – د) | 2حتاب حا د = حا( ب + د) – حا( ب – د) |
2حتاب حتا د = حتا( ب + د) + حتا( ب – د) | 2حاب حا د = حتا( ب – د) – حتا( ب + د) |
أ¯ ب¯ حـ¯
في ∆ أ ب حـ ــــــــــ = ــــــــــ = ــــــــــ = 2 نق
حا أ حاب حاحـ
نق نصف قطر الدائرة الخارجة للمثلث (المارة برؤوسه) |
أ¯ = ب¯حتاحـ + حـ¯حتاب
ب¯ = حـ¯حتاأ + أ¯حتاحـ
حـ¯ = أ¯حتاب + ب¯حتاأ |
| ( أ¯ )2= ( ب¯ )2 + ( حـ¯ )2 – 2 ب¯حـ¯ حتاأ |
( ب¯ )2+ (حـ¯ )2– ( أ¯ )2
حتاأ = ــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2 ب¯حـ¯ |
| ( ب¯ )2= ( حـ¯ )2 + ( أ¯ )2 – 2 حـ¯ أ¯ حتاب | (حـ¯ )2+ ( أ¯ )2– ( ب¯ )2
حتاب= ــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2 حـ¯ أ¯ |
| ( حـ¯ )2= ( أ¯ )2 + ( ب¯ )2 – 2 أ¯ ب¯ حتاحـ | ( أ¯ )2+ (ب¯ )2– ( حـ¯ )2
حتاحـ= ــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2 أ¯ ب¯ |
| المثلث أ ب حـ ، بوضع أ¯ + ب¯ + حـ¯ = 2ح، نق نصف قطر الدائرة الداخلة، ∆ رمز لمساحة المثلث أ ب حـ |
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
∆ = / ح( ح – أ¯ )(ح – ب¯ )(ح – حـ¯ ) |
2 ∆ د 2 ∆ د 2 ∆
حاأ = ـــــــــــــــ، حاب = ـــــــــــــــ ، حاحـ = ـــــــــــــــ
ب¯ حـ¯ حـ¯ أ¯ أ¯ ب¯ |
 |
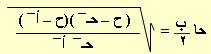 |
 |
 |
 |
 |
 | 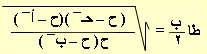 |
 |
ب – حـ ب¯ – حـ¯ أ
طا ـــــــــــــــ = ـــــــــــــــــــــ طتا ــــ
2 ب¯ + حـ¯ 2 |
حـ – أ حـ¯ – أ¯ ب
طا ـــــــــــــــ = ـــــــــــــــــــــ طتا ــــ
2 حـ¯ + أ¯ 2 |
أ – ب أ¯ – ب¯ حـ
طا ـــــــــــــــ = ــــــــــــــــــــ طتا ـــــ
2 أ¯ + ب¯ 2 |
∆
نق = ـــــــ حيث نق نصف قطر الدائرة الداخلة للمثلث
ح |
∆ أ ب
نق = ـــــــ = (ح– أ¯ ) طا ـــ = ( ح – ب¯ ) طاـــــ = ...
ح 2 2 |
أ
نق = (ح – أ¯ ) طا ـــ ، نق نصف قطر الدائرة الداخلة
2 |
∆ أ
نق = ـــــــــــــــ = ح طا ــــ ، نق للدائرة التي تمس أ¯
ح – أ¯ 2
وامتدادي الضلعين الآخرين ، بالمثل للباقي |
∆ ب
نق = ـــــــــــــــ = ح طا ـــ ، نق للدائرة التي تمس ب¯
ح – ب¯ 2
وامتدادي الضلعين الآخرين |
∆ حـ
نق = ـــــــــــــــ = ح طا ـــــ ، نق للدائرة التي تمس حـ¯
ح – حـ¯ 2
وامتدادي الضلعين الآخرين |

